برای فهمیدن عملیات بهره‌برداری از یک سیستم RO ، داشتن شناختی بنیادی از مدل‌های تئوری گوناگون جهت توضیح در مورد حرکت مواد حل‌شده و آب از میان یک غشاء‌RO  ضروری است. به‌وسیله‌ی درک چگونگی انتقال مواد حل شده و آب از میان ممبرین ، اصلاحات مناسبی برای پلیمرهای ممبرین جهت بهبود عملکرد ( شدت نفوذ و مقدار دفع ) ، می‌تواند صورت پذیرد.
این بخش شامل توسعه‌ی مدل‌های انتقال می‌باشد. همچنین پلیمرهای اساسی ممبرین و مدول‌ها ، و چگونگی ساخت هر کدام توضیح داده شده است.

مدل‌های انتقال
هدف یک مدل انتقال این است که مقدار عملکرد را ( معمولاً شدت نفوذ حلال و ماده‌ی حل شده  ) در شرایط بهره‌برداری ( معمولاً نیروهای فشاری ناشی از فشار و غلظت)  به‌صورت رابطه‌ی ریاضی بیان کند. هدف پیش‌بینی رفتار غشاء در شرایط معین می‌باشد.
چندین مدل برای توضیح نحوه‌ی انتقال جرم از میان ممبرین‌های RO وجود دارد. این مدل‌ها مبتنی بر فرضیه‌های متفاوت بوده و دارای درجات مختلفی از پیچیدگی‌ هستند. مدل محلول-نفوذ بهترین توضیح را در مورد عملکرد "درست" و ممبرین‌های بدون نقص ارائه می‌کند، و به‌عنوان تئوری پیشرو در پدیده‌ی انتقال غشائی در نظر گرفته می‌شود. در این‌جا سه تئوری دیگر نیز برای تکمیل شدن بحث مطرح می‌شوند.
مدل‌های انتقال در سه گروه اصلی طبقه‌بندی می‌شوند:‌ مدل‌های مبتنی بر محلول/نفوذ ماده‌ی حل‌شده (مدل‌های انتقال غیر متخلخل) ، مدل‌های مبتنی بر ترمودینامیک برگشت ناپذیر ، و مدل‌های مبتنی بر غشای متخلخل. نکات جالب برخی از این مدل‌ها در زیر توضیح داده شده‌ است.

مدل محلول-نفوذ (مدل غیر متخلخل)
مدل انتقالی محلول-نفوذ در اصل توسط Lonsdale et. al  توضیح داده شد. در این مدل فرض می‌شود که غشاء غیر متخلخل است ( بدون نقایص ). در این نظریه بیان می‌شود که چون ملکول تمایل به حل شدن در غشاء دارد به داخل آن نفوذ کرده و به این دلیل پدیده‌ی انتقال در غشاء رخ می‌دهد. این امر در مورد مولکول‌های حلال و حل شونده در محلول صادق می‌باشد.   
در مدل محلول-نفوذ ، انتقال حلال و حل شونده مستقل از یکدیگر است ، همان‌طوری‌که در معادله‌ی 1 و 2 ملاحظه می‌شود. شدت نفوذ حلال در میان غشاء به‌طور خطی متناسب است با اختلاف فشار مؤثر در سراسر غشاء (معادله‌ی 1):
(1)                                             Jw = A (ΔP – ΔΠ)
که :
Jw = شدت نفوذ حلال
A = ضریب نفوذپذیری آب ( تابعی از مقدار نفوذ آب در میان غشاء )
ΔP = نیروی محرکه‌ی ناشی از اعمال فشار ( تابعی از فشارهای مربوط به خوراک ، محلول غلیظ شده و آب تصفیه شده )
ΔΠ = فشار اسمزی محلول ( تابعی از غلظت‌های مربوط به خوراک ، محلول غلیظ شده و آب تصفیه شده )

شدت نفوذ ماده‌ی حل شده در میان غشاء متناسب است با اختلاف غلظت مؤثر ماده‌ی حل شده در سراسر غشاء ( معادله‌ی 1 ):
(2)                                             Js = K (CA2 – CA3)
که :
Js = شدت نفوذ ماده‌ی حل شده
K = ضریب نفوذپذیری نمک ( تابعی از مقدار نفوذ نمک در میان غشاء )
CA = غلظت مولی ماده‌ی حل شده
زیرنویس‌ها :
2 = در لایه‌ی مرزی
3 = در آب تصفیه شده
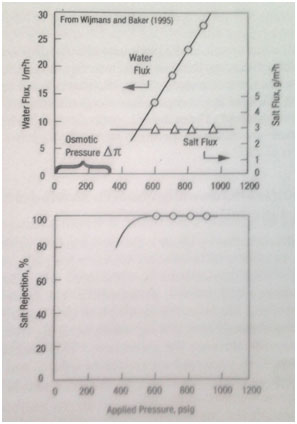
معادلات 1 و 2 معمولی‌ترین معادلاتی هستند که به‌دلیل سادگی و تقریب نزدیک آن‌ها به داده‌های تجربی ، برای توضیح انتقال آب و مواد حل شده را از میان غشاء مورد استفاده قرار می‌گیرند. شکل 1 را در نظر بگیرید ، که شدت نفوذ آب و نمک و نیز مقدار دفع نمک ارائه داده شده توسط ممبرین آب دریا را به‌عنوان تابعی از فشار اعمال شده ، نشان می‌دهد. به‌طور خاص از ممبرین آب دریا FilmTec FT-30 برای محلول کلرید سدیم 35000ppm  با فشار اسمزی 350 psi (2.5 Mpa) استفاده شد. همان‌طور که در شکل نشان داده شده است ، تا فشار اعمال شده از فشار اسمز بیشتر نشود ، واقعاً هیچ آبی نفوذ نمی‌کند. به‌محض آغاز شدن نفوذ آب ، این مقدار به‌طور خطی با افزایش فشار زیاد می‌شود ، همان‌طوری‌که با معادله‌ی 1 پیش‌بینی شده بود. از طرف دیگر ، شدت نفوذ نمک در محدوده‌ی فشار اعمال شده نسبتاً ثابت باقی می‌ماند ، همان‌طوری‌که با معادله‌ی 1 پیش‌بینی شده بود. بنابراین ، همان‌طور‌که فشار اعمال شده افزایش می‌یابد ، به‌تدریج آب بیشتری نسبت به نمک از میان غشاء عبور می‌کند.



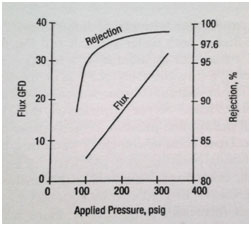
 از این مطالب می‌توان نتیجه گرفت که غلظت نمک در آب تصفیه شده با افزایش فشار اعمال شده کم می‌شود. همان‌طور که غلظت در آب تصفیه شده کاهش می‌یابد ، درصد دفع نمک با افزایش فشار اعمال شده به 100درصد نزدیک می‌شود. در واقع این مسئله در شکل 1 نشان داده شده است. این نتایج برای ممبرین فشار پایین که برای محلول کلرید سدیم 5000ppm  در 25 درجه سانتی‌گراد به‌کار برده شده است ، مانند شکل 2 ، صادق می‌باشد.

مدل محلول-نفوذ ناقص ( مدل متخلخل )
نظریه‌ی محلول-نفوذ عملکرد ممبرین کامل را مدل‌سازی می‌کند. در حالت واقعی ، ممبرین‌های صنعتی درگیر نقایصی هستند ، آن‌چنان‌که در زمان شکل گرفتن‌ تئوری کاملی که عملکرد را مدل‌سازی می‌کند ، برخی از مباحث را باید در نظر گرفت. اساس مدل نفوذ ناقص ، فرض وجود نقایصی جزئی در ممبرین است که در طی عملیات ساخت بوجود آمده‌اند ، آن‌چنان‌که محلول بتواند از میان ممبرین تراوش کند. این مدل به توضیح در مورد کمتر بودن مقدار طراحی شده‌ی جداسازی مواد حل شده و آب نسبت به مقدار پیش‌بینی‌شده توسط مدل محلول – نفوذ ، غیر متخلخل ، که در ممبرین‌های صنعتی مشاهده شده است ، کمک می‌کند.
شدت نفوذ آب از میان ممبرین با استفاده از معادله‌ی 3 به‌دست می‌آید. این شدت نفوذ مبتنی بر مدل محلول - نفوذ به‌علاوه‌ی عبارت انتقال برعکس به‌علت وجود محل‌های معیوب ، می‌باشد.
(3)                      Nw = Jw + K3 ΔPCw = A ( ΔP – ΔΠ ) + K3 ΔPCw
که :
Nw = شدت نفوذ کلی آب
K3 = ضریب کوپلینگ
Cw = غلظت آب در سمت مربوط به خوراک ممبرین
شدت نفوذ ماده‌ی حل‌شده از معادله‌ی 4 به‌دست می‌آید :
(4)            Ns = Js + K3 ΔPCR = K ( CA2 – CA3 ) + K3 ΔPCR          
که :
Ns = شدت نفوذ کلی ماده‌ی حل‌شده
CR = غلظت ماده‌ی حل‌شده در سمت مربوط به خوراک ممبرین
بار دیگر ، شدت نفوذ ماده‌ی حل‌شده مساوی با مقدار حاصل از مدل نفوذ- محلول ( معادلات 1 و 2 ) به‌علاوه‌ی عبارت شدت جریان نشان داده شده از میان محل‌های معیوب می‌باشد.
آزمایشات نشان داده‌اند که مدل محلول – نفوذ ناقص نسبت به مدل محلول – نفوذ به‌تنهایی ، با داده‌ها تناسب بیشتری داشته و از دیگر مدل‌های جریان متخلخل نیز بهتر می‌باشد. به‌هرحال ، اغلب به‌دلیل سادگی به مدل محلول – نفوذ استناد می‌شود که حقیقتاً عملکرد غشاء بدون نقص  RO را به‌دقت الگوسازی می‌کند.

مدل منافذ ریز (مدل متخلخل)
مدل منافذ ریز مبتنی‌بر تعادل نیروهای اعمال‌شده و اصطکاکی در یک منفذ یک بعدی می‌باشد. در این مدل به اصطکاک بین ماده‌ی حل‌شده و محلول و نیز اصطکاک بین ماده‌ی حل‌شده و جسم غشاء توجه می‌شود. همچنین این مدل دربرگیرنده‌ی ضخامت غشاء و کسر سطح منفذ نسبت به سطح غشاء می‌باشد.
در اینجا ، به‌دلیل پیچیدگی این مدل ، به‌صورت ریاضی آن‌را نشان نداده‌ایم ، اما به خوانندگان توصیه‌می‌شود که برای جزئیات بیشتر به منابع معرفی‌شده رجوع نمایند.

مدل جذب ترجیحی – جریان مویرگی ( مدل متخلخل )
این مدل مبتنی‌بر مدل تعمیم‌یافته‌ی جریان مویرگی می‌باشد که شامل جریان ویسکوز برای آب و انتقال مواد حل‌شده ، و نیز برای نفوذ از طریق خلل و فرج است. این مدل بیشتر متکی به تئوری فیلم جهت انتقال از میان لایه‌های مرزی می‌باشد. در این مدل توضیح داده می‌شود که به‌وسیله‌ی وارد نمودن فشار ، هم حلال و هم جسم حل‌شده به‌داخل منافذ بسیار ریز غشاء نفوذ می‌کنند ، به‌همراه آبی که ترجیحاً جذب دیواره‌های منافذ می‌گردد. به‌دلایل فیزیک وشیمیایی ، نمک از سطح غشاء‌ دفع می‌شود. فرآیند انتقال در میان غشاء تنها از طریق منافذ انجام می‌پذیرد.
شدت نفوذ حلال توسط معادله‌ی 1 محاسبه می‌شود ، که در آن فرآیند انتقال با نیروی محرکه‌ی ناشی از فشار متناسب است. شدت نفوذ کلی ماده‌ی حل‌شده بستگی به مقدار نفوذ دارد و به‌وسیله‌ی معادله‌ی 5 محاسبه می‌گردد :
(5)                           NS = (DAM K / T)(CA2 – CA3)            
که :
DAM = مقدار نفوذ ماده‌ی حل‌شده به‌داخل غشاء
T = ضخامت مؤثر غشاء
CA2 = غلظت مولی ماده‌ی حل‌شده در لایه‌ی مرزی
CA3 = غلظت مولی ماده‌ی حل‌شده در جریان نفوذ کرده

مطالعه‌ی پدیده‌ی وابسته به انتقال (ترمودینامیک برگشت‌ناپذیر)
پدیده‌های وابسته به انتقال را می‌توان حتی بدون داشتن هرگونه دانشی در رابطه با مکانیزم‌های انتقال از میان غشاء یا هرگونه اطلاعاتی درباره‌ی ساختار غشاء مطالعه‌ نمود. در اساس ترمودینامیک برگشت‌ناپذیر فرض می‌شود که اگر سیستم به زیرمجموعه‌هایی به‌اندازه‌ی کافی کوچک تقسیم شود تا تعادل محلی به‌وجود آید ، می‌توان معادلات ترمودینامیکی را برای چنین زیرمجموعه‌هایی نوشت.
مانند مدل منافذ ریز ، بیان ریاضی شدت نفوذ‌های حلال و ماده‌ی حل‌شده برای مدل ترمودینامیک برگشت‌ناپذیر بسیار پیچیده بوده و فراتر از این متن می‌باشد. به‌هرحال توصیه‌می‌شود که خوانندگان برای جزئیات بیشتر به منابع معرفی‌شده رجوع نمایند.


برچسپ: